Peluang

1. Percobaan, ruang sampel, dan kejadian

• Percobaan (dalam studi peluang) didefinisikan sebagai suatu proses dengan hasil dari suatu kejadian bergantung pada kesempatan. Ketika percobaan diulangi, hasil-hasil yang diperoleh tidak selalu sama, walaupun dilakukan dengan kondisi yang tepat sama dan secara hati-hati. Percobaan seperti ini disebut percobaan acak.
• Ruang sampel adalah himpunan dari semua hasil yang mungkin dari suatu percobaan. Ruang sampel dinotasikan dengan S. Banyaknya elemen ruang sampel dinyatakan dengan \(n(S)\).
• Kejadian atau peristiwa adalah himpunan bagian dari ruang sampel, biasanya dinotasikan dengan huruf kapital seperti \(A, B, C\), dan seterusnya. Banyaknya elemen kejadian \(A\) dinyatakan dengan \(n(A)\), banyaknya elemen kejadian \(B\) dinyatakan dengan \(n(B)\), dan sebagainya.

Contoh:
Dari percobaan mengundi dengan sebuah dadu, tentukan:
a. ruang sampel percobaan tersebut,
b. kejadian \(A\), yaitu munculnya sisi dadu bermata ganjil,
c. kejadian \(B\), yaitu munculnya sisi dadu yang habis dibagi 3 .

Penyelesaian:
a. Hasil-hasil yang mungkin dari percobaan mengundi dengan sebuah dadu adalah munculnya sisi dadu bermata \(1,2,3,4,5\), dan 6 . Jadi, ruang sampelnya adalah \(S=\{1,2,3,4,5,6\}\) dan banyaknya elemen ruang sampel \(n(S)=6\).
b. Kejadian munculnya sisi dadu bermata ganjil adalah \(A=\{1,3,5\}\) sehingga \(n(A)=3\).
c. Kejadian munculnya sisi dadu yang habis dibagi 3 adalah \(B=\{3,6\}\) sehingga \(n(B)=2\).

2. Peluang suatu kejadian

Dalam hidup, sering kali, kita dihadapkan pada berbagai pilihan. Dari berbagai pilihan tersebut, muncul beberapa kemungkinan yang akan dipilih. Sebagai contoh:
a. Saat seseorang mengikuti ujian Matematika, ada dua kemungkinan yang akan terjadi, yaitu lulus atau tidak lulus.
b. Untuk seorang ibu hamil, kemungkinan bayi yang lahir berjenis kelamin laki-laki atau perempuan. Jika bayinya kembar dua, ada 3 kemungkinan jenis kelamin bayinya, yaitu laki-laki dan perempuan, keduanya laki-laki, atau keduanya perempuan.

Diketahui \(S\) adalah ruang sampel dengan banyak elemen \(n(S)\) dan \(A\) adalah suatu kejadian dengan banyak elemen \(n(A)\). Peluang kejadian \(A\), diberi notasi \(P(A)\), ditentukan dengan \(P(A)=\frac{n(A)}{n(S)}\).

3. Kisaran nilai peluang

Jika \(A\) adalah suatu kejadian dengan banyak elemen \(n(A)\), maka banyak elemen \(A\) paling sedikit adalah 0 dan paling banyak sama dengan banyak elemen ruang sampel, yaitu \(n(S)\).
Dalam persamaan, dinyatakan dengan: \(0 \leq n(A) \leq n(S)\)
Jika kedua ruas dibagi dengan \(n(S)\), diperoleh: \(\frac{0}{n(S)} \leq \frac{n(A)}{n(S)} \leq \frac{n(S)}{n(S)} \Leftrightarrow 0 \leq P(A) \leq 1\).
Persamaan tersebut menyatakan kisaran nilai peluang, yaitu suatu angka yang terletak di antara 0 dan 1.
– Nilai \(P(A)=0\) adalah kejadian mustahil, karena kejadian ini tidak mungkin terjadi.
– Nilai \(P(A)=1\) adalah kejadian pasti, karena kejadian ini selalu terjadi.

Coba Anda bayangkan, kejadian yang mustahil terjadi, tidak mungkin terjadi, sangat impossible terjadi, maka peluangnya tidak ada.

Contoh:
Pada pengundian dengan sebuah dadu, tentukan:
a. peluang muncul mata dadu ganjil,
b. peluang muncul mata dadu kurang dari 3 .

Penyelesaian:
Ruang sampel pengundian dengan sebuah dadu \(S=\{1,2,3,4,5,6\}\) sehingga \(n(S)=6\).
a. Misalkan \(A\) adalah kejadian muncul mata dadu ganjil, maka \(A=\{1,3,5\}\) sehingga \(n(A)=3\). Jadi, peluang \(A\) adalah \(P(A)=\frac{n(A)}{n(S)}=\frac{3}{6}=\frac{1}{2}\).
b. Misalkan \(B\) adalah kejadian muncul mata dadu kurang dari 3 , maka \(B=\{1,2\}\) sehingga \(n(B)=2\). Jadi, peluang \(B\) adalah \(P(B)=\frac{n(B)}{n(S)}=\frac{2}{6}=\frac{1}{3}\).

4. Frekuensi harapan

Frekuensi harapan suatu kejadian adalah harapan banyaknya kejadian yang dapat terjadi dari banyak percobaan yang dilakukan.

Jika \(A\) adalah suatu kejadian dan \(P(A)\) adalah peluang terjadinya \(A\), maka besarnya frekuensi harapan kejadian \(A\) dalam \(n\) kali percobaan dirumuskan sebagai:
\[
F(A)=P(A) \times n
\]

Contoh:
Pengundian dengan sekeping logam dilakukan sebanyak 60 kali. Berapa frekuensi harapan muncul sisi gambar?
Penyelesaian:
Pada pengundian dengan sekeping logam, peluang muncul sisi gambar adalah \(P(G)=\frac{1}{2}\). Jadi, frekuensi harapan muncul sisi gambar dalam 60 kali percobaan:
\[
F(G)=\frac{1}{2} \times 60=30 \text { kali }
\]

5. Peluang kejadian majemuk

Jika dua atau lebih kejadian dioperasikan sehingga membentuk kejadian baru, maka kejadian baru ini disebut kejadian majemuk.
a. Peluang komplemen dari suatu kejadian

Jika \(A\) adalah suatu kejadian dan \(A^c\) adalah komplemen dari kejadian \(A\), maka berlaku \(P(A)+P\left(A^C\right)=1\) atau \(P\left(A^{\top}\right)=1-P(A)\).

Contoh:
Dari satu set kartu bridge, diambil sebuah kartu secara acak. Tentukan peluang terambil bukan kartu As.
Penyelesaian:
Satu set kartu bridge berjumlah 52 kartu, berarti \(n(S)=52\).
Misalkan \(B\) adalah kejadian terambil bukan kartu As. Komplemen dari \(B\), yaitu \(B^c\), adalah kejadian yang terambil kartu As. Oleh karena itu, \(n\left(B^C\right)=4\) dan peluang kejadian \(B^c\) adalah sebagai berikut.
\[
P\left(B^C\right)=\frac{n\left(B^c\right)}{n(S)}=\frac{4}{54}=\frac{1}{13}
\]

Jadi, peluang kejadian \(B\), yaitu peluang yang terambil bukan kartu As adalah sebagai berikut.
\[
P(B)=1-P\left(B^C\right)=1-\frac{1}{13}=\frac{12}{13}
\]

b. Penjumlahan peluang

Misalkan percobaan pengundian dengan dua dadu bersamaan. Misalkan kejadian \(A\) adalah jumlah mata dadu yang muncul sama dengan 4 dan kejadian \(B\) adalah jumlah mata dadu yang muncul sama dengan 10. Jadi, \(A=\{(1,3),(2,2),(3,1)\}\) daṇ \(B=\{(4,6),(5,5),(6,4)\}\).
Tampak bahwa tidak satu pun elemen \(A\) yang sama dengan elemen \(B\). Kejadian \(A\) dan \(B\) dalam hal ini disebut sebagai kejadian saling lepas.
Jadi, dua kejadian dikatakan saling lepas apabila tidak ada satu pun elemen yang sama dari keduanya. Dalam notasi himpunan, dua kejadian saling lepas jika \(A \cap B=\varnothing\) atau \(n(A \cap B)=0\).

Kejadian \(A\) dan \(B\) saling lepas

\(
A \cap B=\varnothing \text { atau } n(A \cap B)=0
\)

Kejadian \(A\) dan \(B\) tidak saling lepas

\[
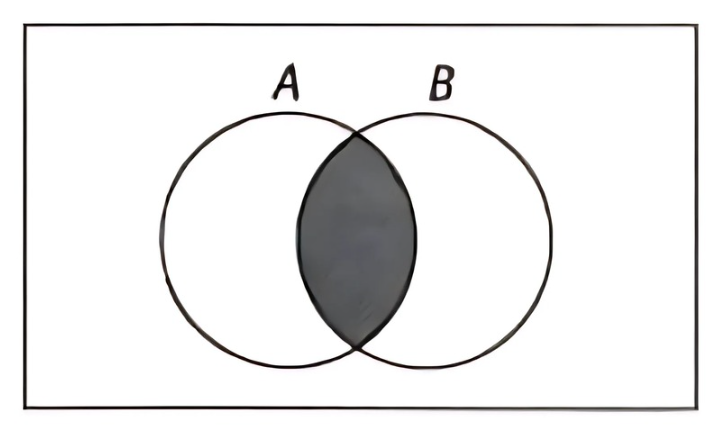
A \cap B \neq \emptyset \text { atau } n(A \cap B) \neq 0
\]

Untuk \(A\) dan \(B\) dua kejadian saling lepas, berlaku

\[
P(A \cup B)=P(A)+P(B)
\]

Untuk \(A\) dan \(B\) dua kejadian tidak saling lepas \([(A \cap B) \neq \varnothing]\), berlaku

\[
P(A \cup B)=P(A)+P(B)-P(A \cap B)
\]

Contoh Kejadian saling lepas:
Dalam pengundian dengan dua dadu secara bersamaan, tentukan peluang muncul mata dadu berjumlah 4 atau 10.
Penyelesaian:
Pada pengundian dengan dua dadu bersamaan, banyak hasil yang mungkin adalah 36 sehingga \(n(S)=36\).
Kejadian \(A=\) muncul mata dadu berjumlah 4, maka \(A=\{(1,3),(2,2),(3,1)\}\) dan \(n(A)=3\)
Kejadian \(B=\) muncul mata dadu berjumlah 10 , maka \(B=\{(4,6),(5,5),(6,4)\}\) dan \(n(B)=3\)
Kejadian \(A\) dan \(B\) tidak memiliki satu pun elemen yang sama, berarti \(A\) dan \(B\) saling lepas. Jadi, peluang gabungan \(A\) dan \(B\) adalah sebagai berikut.

\[
P(A \cup B)=P(A)+P(B)=\frac{n(A)}{n(S)}+\frac{n(B)}{n(S)}=\frac{3}{36}+\frac{3}{36}=\frac{6}{36}=\frac{1}{6}
\]

Contoh Kejadian tidak saling lepas:
Sebuah kartu diambil secara acak dari satu set kartu bridge. Tentukan peluang yang terambil adalah kartu sekop atau kartu As.
Penyelesaian:
Satu set kartu bridge terdiri atas 52 kartu yang berbeda, sehingga \(n(S)=52\).
Misalkan kejadian A menyatakan terambil kartu sekop.
Banyak kartu sekop \(=13\) sehingga \(n(A)=13\).
Misalkan kejadian \(B\) menyatakan terambil kartu As.
Banyak kartu \(A s=4\) sehingga \(n(B)=4\).
Kejadian \(A\) dan \(B\) memiliki satu elemen yang sama, karena salah satu jenis kartu As adalah sekop. Jadi, \(A\) dan \(B\) dua kejadian tidak saling lepas dengan \(A \cap B=\{\) kartu As sekop \(\}\) dan \(n(A \cap B)=1\).
Peluang gabungan \(A\) dan \(B\) adalah sebagai berikut.
\[
P(A \cup B)=P(A)+P(B)-P(A \cap B)=\frac{n(A)}{n(S)}+\frac{n(B)}{n(S)}-\frac{n(A \cap B)}{n(S)}=\frac{13}{52}+\frac{4}{52}-\frac{1}{52}=\frac{16}{52}=\frac{4}{13}
\]

c. Perkalian peluang

Dua kejadian dikatakan saling bebas jika munculnya kejadian pertama tidak mempengaruhi peluang munculnya kejadian kedua.

Jika \(A\) dan \(B\) dua kejadian saling bebas, maka peluang kejadian \(A\) dan \(B\) ditulis \(P(A \cap B)\), ditentukan dengan \(P(A \cap B)=P(A) \times P(B)\).

Jika \(A\) dan \(B\) dua kejadian bersyarat, maka peluang kejadian \(A \operatorname{dan} B\) ditulis \(P(A \cap B)\) ditentukan dengan \(P(A \cap B)=P(A) \times P(B \mid A)\),
dengan \(P(B \mid A)\) adalah peluang kejadian \(B\) jika diketahui kejadian \(A\) telah terjadi.

Contoh Dua kejadian saling bebas:
Dalam sebuah rak buku, terdapat 6 buku matematika dan 8 buku kimia. Dua buku diambil secara acak dari rak buku tersebut secara satu per satu. Jika buku pertama yang diambil dikembalikan ke rak buku sebelum buku kedua diambil, tamtukan peluang yang terambil:
a. buku pertama matematika dan buku kedua kimia
b. buku pertama kimia dan buku kedua kimia

Penyelesaian:
Rak buku berisi 14 buku ( 6 buku matematika dan 8 buku kimia), sehingga \(n(S)=14\).
Misalkan \(A=\) kejadian terambil buku matematika, maka \(P(A)=\frac{n(A)}{n(S)}=\frac{6}{14}=\frac{3}{7}\) dan
\[
B=\text { kejadian terambil buku kimia, maka } P(A B)=\frac{n(B)}{n(S)}=\frac{8}{14}=\frac{4}{7}
\]
a. Peluang terambil buku matematika, kemudian buku kimia
\[
P\left(A_1 \cap B_2\right)=P(A) \times P(B)=\frac{3}{7} \times \frac{4}{7}=\frac{12}{49}
\]
b. Peluang terambil buku kimia, kemudian buku kimia
\[
P\left(B_1 \cap B_2\right)=P(B) \times P(B)=\frac{4}{7} \times \frac{4}{7}=\frac{16}{49}
\]

Contoh Dua kejadian bersyarat:
Sebuah kotak berisi 6 bola merah dan 4 bola biru. Jika diambil 2 bola satu per satu tanpa pengembalian, tentukan peluang bola yang terambil berturut-turut berwarna biru dan merah.

Penyelesaian:
Banyak bola sebelum pengambilan adalah 6 bola merah +4 bola biru \(=10\) bola
Pada pengambilan pertama, terambil bola biru. Tersedia 4 bola biru dari 10 bola, sehingga peluang terambil bola biru \(P(B)\) adalah \(P(B)=\frac{4}{10}=\frac{2}{5}\).
Banyak bola sebelum pengambilan kedua adalah 6 bola merah +3 bola biru \(=9\) bola
Peluang terambil bola merah dengan syarat bola biru telah terambil pada pengambilan pertama ditulis \(P(M \mid B)\) adalah \(P(M \mid B)=\frac{6}{9}=\frac{2}{3}\)
Jadi, peluang terambil berturut-turut bola berwarna biru dan merah adalah sebagai berikut.
\[
P(B \cap M)=P(B) \times P(M \mid B)=\frac{2}{5} \times \frac{2}{3}=\frac{4}{15}
\]